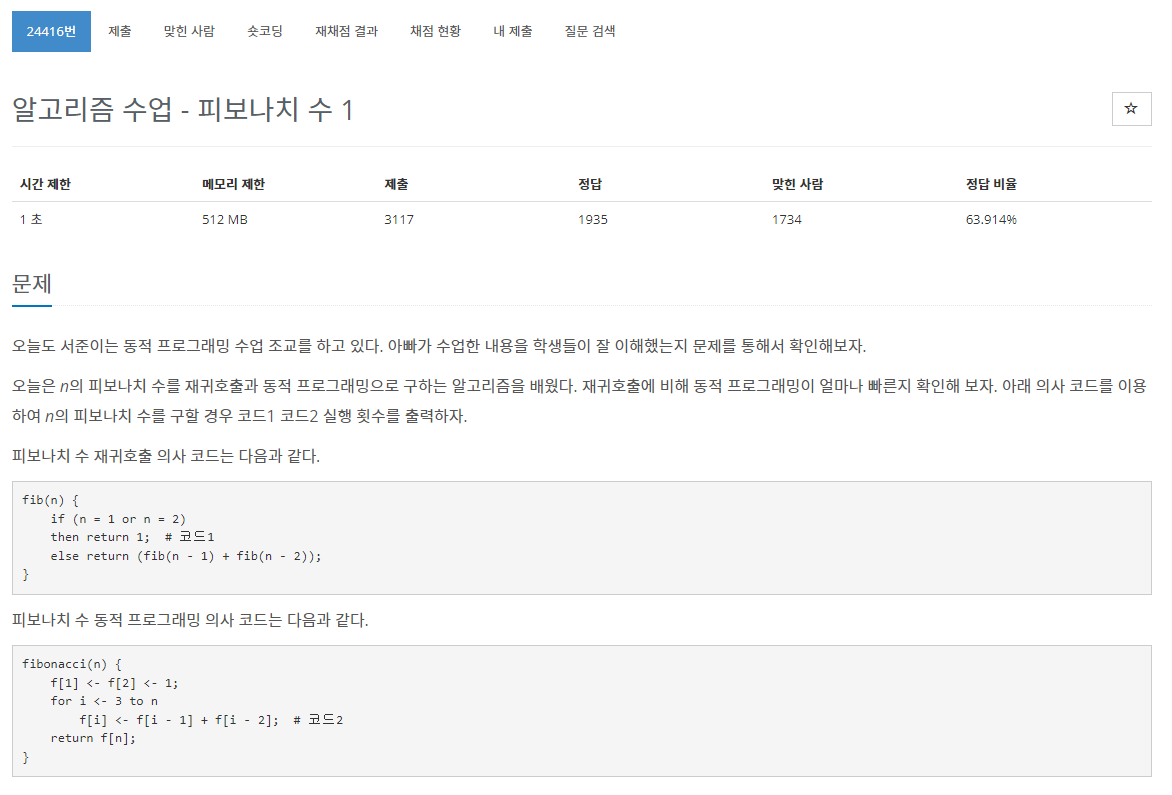
문제
정리
* 재귀
1
2
3
4
5
6
7
8
9
public static int fib_recursion(int n) {
cnt++;
if(n == 1 || n == 2) {
return 1;
} else {
return fib_recursion(n-1) + fib_recursion(n-2);
}
}
자기자신을 반복해서 호출
f(n)을 구하기 위해 f(n-1), f(n-2)를 구하고 f(n-1), f(n-2)는 다시 쪼개지면서 f를 다시 호출하지 않을때까지 반복하는 방식(하향식)
fib(5) = fib(4) + fib(3)
= fib(3) + fib(2) + fib(3) = fib(2) + fib(1) + fib(2) + fib(2) + fib(1)
= 3*fib(2) + 2*fib(1)
fib(4) = fib(3) + fib(2)
fib(3) = fib(2) + fib(1)
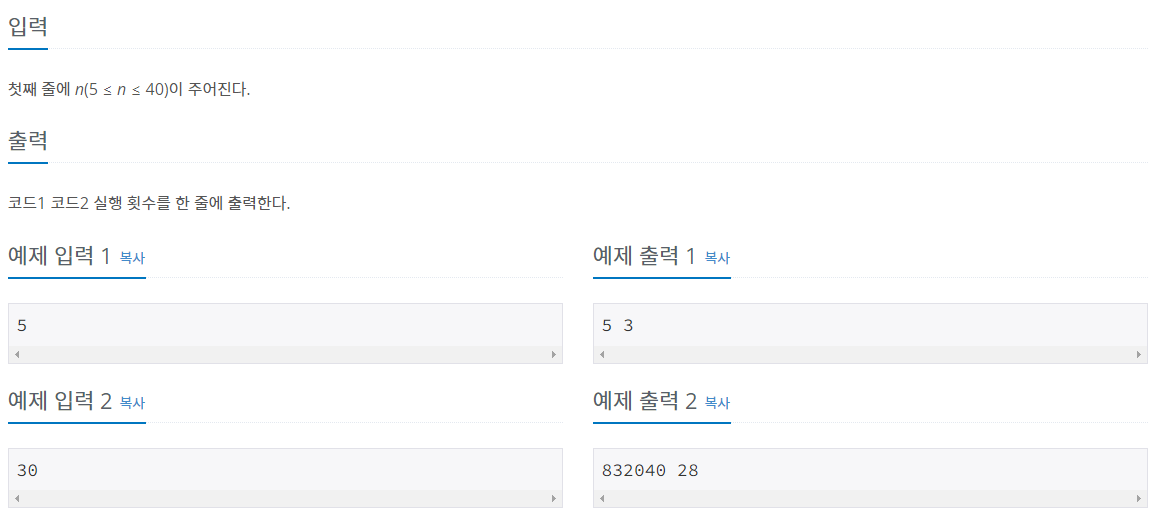
n=5 일 경우 함수 호출 9번 발생
n=30 일 경우 함수 1664079번 호출
* DP(Dynamic Programming)
1
2
3
4
5
6
7
8
9
10
11
12
13
public static int fib_dp(int n) {
int[] dp = new int[n+1];
dp[1] = 1;
dp[2] = 1;
for(int i=3; i<=n; i++) {
cnt++;
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장해서 동일한 계산의 반복 수행을 제거하는 방법
1부터 n까지 올라가면서 각 단계의 값을 메모리에 저장해서 다음 단계의 값을 구할때 사용(상향식)
dp[3] = dp[2] + dp[1] = 1 + 1 = 2
dp[4] = dp[3] + dp[2] = 2 + 1 = 3
dp[5] = dp[4] + dp[3] = 3 + 2 = 5
n=5 일 경우 for문 3번 반복
n=30 일 경우 for문 28 반복
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
package acmicpc;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
public class acmicpc24416 {
static int cnt = 0;
public static void main(String[] agrs) {
try {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(reader.readLine());
fib_recursion(n);
writer.append(String.valueOf(cnt) + " ");
cnt=0;
fib_dp(n);
writer.append(String.valueOf(cnt));
writer.flush();
writer.close();
} catch (Exception e) {
}
}
public static int fib_recursion(int n) {
if(n == 1 || n == 2) {
cnt++;
return 1;
} else {
return fib_recursion(n-1) + fib_recursion(n-2);
}
}
public static int fib_dp(int n) {
int[] dp = new int[n+1];
dp[1] = 1;
dp[2] = 1;
for(int i=3; i<=n; i++) {
cnt++;
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
}
